dynamic order-preserving 的数据结构中,最简单的就是 sorted linked list,所有操作的复杂度均在
O(n),性能较 B+ Tree 相比逊色许多,但如果将多个 sorted linked list 垒起来,就可能提供与 B+ Tree 相媲美的性能
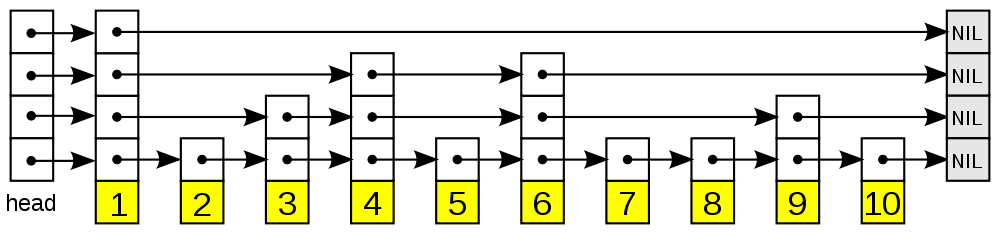
- 表头(head):负责维护跳跃表的节点指针。
- 跳跃表节点:保存着元素值,以及多个层。
- 层:保存着指向其他元素的指针。高层的指针越过的元素数量大于等于低层的指针,为了提高查找的效率,程序总是从高层先开始访问,然后随着元素值范围的缩小,慢慢降低层次。
- 表尾:全部由
NULL组成,表示跳跃表的末尾。
技巧💡
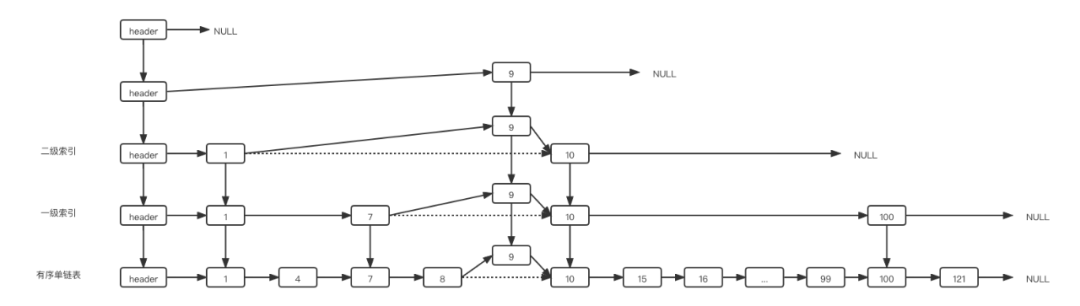
跳表的本质:是对有序链表的改造,为单链表加多层索引,以空间换时间的策略,解决了单链表中查询速度的问题,同时也能快速实现范围查询。
时间复杂度 O(logn) 空间复杂度: O(n)
代码实现与解析
数据结构
- SkipList 用于保存跳跃表节点的相关信息, 比如节点的数量, 以及指向表头节点和表尾节点的指针。
- Node 节点用来表示跳跃表的节点。其中levels,是层级。
- Level 层级,是Node的结构,代表层级。层级指向下一个Node。在查询遍历的时候,就是根据这个进行查找。
type Node struct {
value uint32
levels []*Level // 索引节点,index=0是基础链表
}
type Level struct {
next *Node
}
type SkipList struct {
header *Node // 表头节点
length uint32 // 原始链表的长度,表头节点不计入
height uint32 // 最高的节点的层数
}
func NewSkipList() *SkipList {
return &SkipList{
header: NewNode(MaxLevel, 0),
length: 0,
height: 1,
}
}
func NewNode(level, value uint32) *Node {
node := new(Node)
node.value = value
node.levels = make([]*Level, level)
for i := 0; i < len(node.levels); i++ {
node.levels[i] = new(Level)
}
return node
}多少层合适?
跳跃表的难点,在于层级问题。即多少层合适。太多和太少都不太行。一般控制每层的概念是下一层的1/2. 如:
L1 1/2
L2 1/4
….
那如何实现呢?直接用用随机函数。判断连续出现1的概率。
const p = 0.5
func (sl *SkipList) randomLevel() int {
level := 1
r := rand.New(rand.NewSource(time.Now().UnixNano()))
for r.Float64() < p && level < MaxLevel {
level++
}
return level
}查找
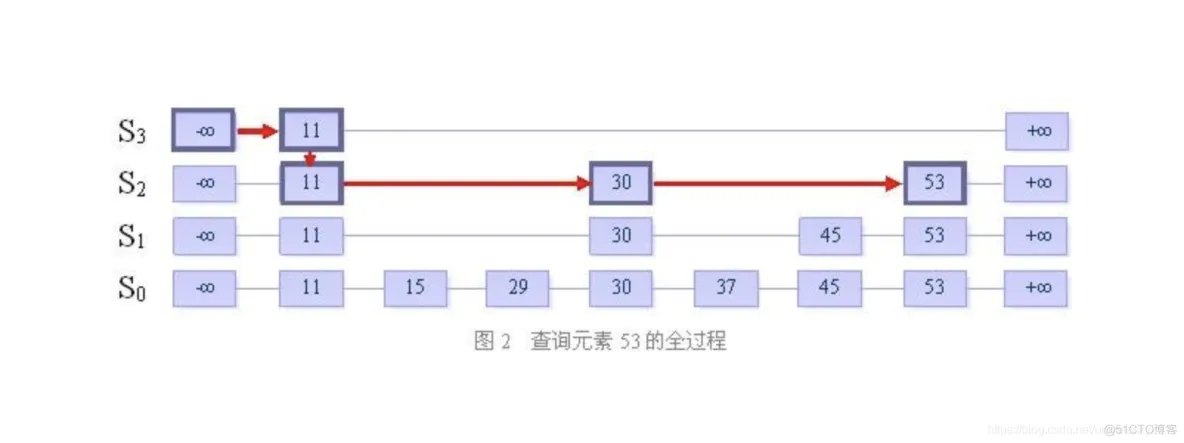
查找的时候,从右上角header的最高层级开始开始查找。
- 当前层级向下一个节点查找,直至下节点>待查找的值,或者已经是最后一个节点。
- 当前节点>待查找的值时,进行到下一个层级。
func (sl *SkipList) Find(value uint32) *Node {
tmp := sl.header
// 从高往低层遍历查询
for i := int(sl.height); i > 0; i-- {
// 当前层,向右查找。 这里key用<=,主要是与后面的插入方法相同逻辑
for tmp.levels[i].next != nil && tmp.levels[i].next.value < value {
tmp = tmp.levels[i].next
}
if tmp.levels[i].next != nil && tmp.levels[i].next.value == value {
return tmp
}
}
return nil
}插入

插入的逻辑和查找是类似的,找到需要插入的地方。然后将待插入位置节点的值临时记录到update数组中。
- 保存需要待插入的位置,并记录到update[i]中
- 生成层级,创建节点值
- 节点的所有层级的下一个节点指向 update[i].next。
- 原来的节点的next,更新为当前节点。
- 特殊处理,层级变高的情况。
func (sl *SkipList) Insert(value uint32) (result bool) {
result = false
update := make([]*Level, MaxLevel)
tmp := sl.header
for i := int(sl.height); i > 0; i-- {
// 当前层,向右查找
for tmp.levels[i].next != nil && tmp.levels[i].next.value < value {
tmp = tmp.levels[i].next
}
// 不支持重复
if tmp.levels[i].next.value == value {
return
}
update[i] = tmp.levels[i]
}
newLevel := sl.randomLevel()
node := NewNode(uint32(newLevel), 0)
for i := 0; i < newLevel; i++ {
// 说明新节点层数超过了跳表当前的最高层数,此时将头节点对应层数的后继节点设置为新节点
if update[i].next == nil {
sl.height++
sl.header.levels[i].next = node
continue
}
node.levels[i].next = update[i].next
update[i].next = node
}
sl.length++
result = true
return
}删除
删除,和插入的逆向操作。找到要删除的节点和上一个节点的信息。然后进行逆操作。如果层级降低了,还要减低层级
func (sl *SkipList) Delete(value uint32) bool {
var node *Node
last := make([]*Node, sl.height)
tmp := sl.header
for i := int(sl.height) - 1; i >= 0; i-- {
for tmp.levels[i].next != nil && tmp.levels[i].next.value < value {
tmp = tmp.levels[i].next
}
last[i] = tmp
// 拿到 value 对应的 node
if tmp.levels[i].next!=nil&&tmp.levels[i].next.value == value {
node = tmp.levels[i].next
}
}
// 没有找到 value 对应的 node
if node == nil {
return false
}
// 找到所有前置节点后需要删除node
for i := 0; i < len(node.levels); i++ {
last[i].levels[i].next = node.levels[i].next
node.levels[i].next = nil
}
// 重定向跳表高度
for i := 0; i < len(sl.header.levels); i++ {
if sl.header.levels[i].next == nil {
sl.height = uint32(i)
break
}
}
sl.length--
return true
}开源源码应用
redis zset
Redis 为什么这么快? Redis 的有序集合 zset 的底层实现原理是什么? —— 跳跃表 skiplist_51CTO博客_redis的有序集合底层实现
技巧💡
redis中,跳表只在zset结构有使用。
- 当数据较少的时候,zset是由一个ziplist来实现的
- 当数据较多的时候,zset是一个由dict 和一个 skiplist来实现的,dict用来查询数据到分数的对应关系,而skiplist用来根据分数查询数据。
struct zset{
// 跳跃表
zskiplit *zsl;
// 字典, 存储的key是 数据,value是score
dict *dice;
};
struct zskiplistNode {
// 真实数据指针,存放节点数据,存放string robj
robj *obj;
// 节点的分数
double score;
// 上一个节点,向前一个节点的指针,节点只有一个向前指针,最底层是一个双向链表
zskiplistNode *backward;
// 层级,存放各层链表的向后指针结构
zskiplistLevel level[];
}
// 包含一个forward ,指向对应层后一个节点
struct zskiplistLevel{
// 下一个指针
zskiplistNode *forward;
// 跨度,用于排名用
unsinged int span;
}
struct zskiplistNode{
// 头节点、尾节点
zskiplistNode *header, *tail;
// 节点数量
long length;
// 层级
int level;
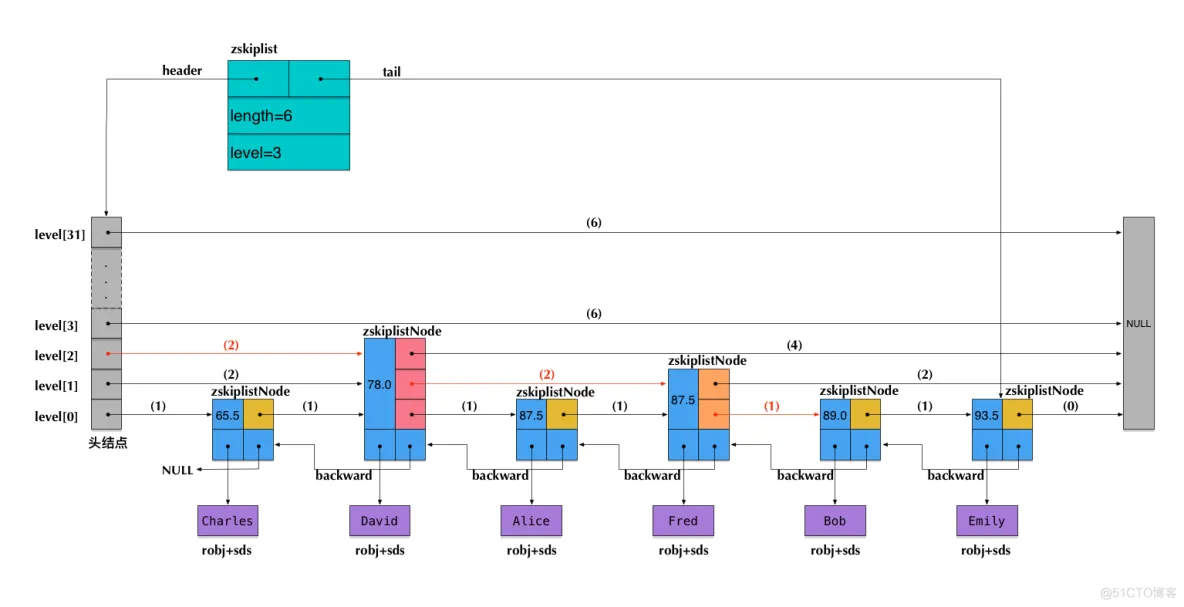
}从结构定义可以看出,与经典跳跃表的差异。
- 新增了 backward,支持双向指针
- Level新增了span,跨度,方便计算排名。
redis的跳跃表的优化
- 经典跳表不支持重复值,redis跳表支持重复的分值score
- redis跳表的排序是根据score和成员对象两者共同决定的。zset还维护了一个map,保存成员对象与分值的映射关系,被用来通过成员对象快速查找分值,定位对应的节点,在ZRANK、ZREVRANK、ZSCORE等命令中均有使用。
- redis跳表的原链表是个双向链
zset中的dict
zset还维护了一个map,保存成员对象与分值的映射关系,被用来通过成员对象快速查找分值,定位对应的节点,在ZRANK、ZREVRANK、ZSCORE等命令中均有使用。
另外,这个map还用于插入节点时,判断是否存在重复的成员对象。见下面redis源码中的dictFind函数。
int zsetAdd(robj *zobj, double score, sds ele, int in_flags, int *out_flags, double *newscore) {
// ...
/* Update the sorted set according to its encoding. */
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
// ...
} else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) {
zset *zs = zobj->ptr;
zskiplistNode *znode;
dictEntry *de;
de = dictFind(zs->dict,ele);
if (de != NULL) {
// 已经存在
// ...
} else if (!xx) {
// 不存在,插入
ele = sdsdup(ele);
znode = zslInsert(zs->zsl,score,ele);
serverAssert(dictAdd(zs->dict,ele,&znode->score) == DICT_OK);
*out_flags |= ZADD_OUT_ADDED;
if (newscore) *newscore = score;
return 1;
} else {
*out_flags |= ZADD_OUT_NOP;
return 1;
}
}
}资料
Tree Indexes - open-courses
带你彻底击溃跳表原理及其Golang实现!(内含图解)-轻识
golang泛型实现——skiplist-原创手记-慕课网
深入理解Redis跳跃表的基本实现和特性 - 掘金