字符串匹配
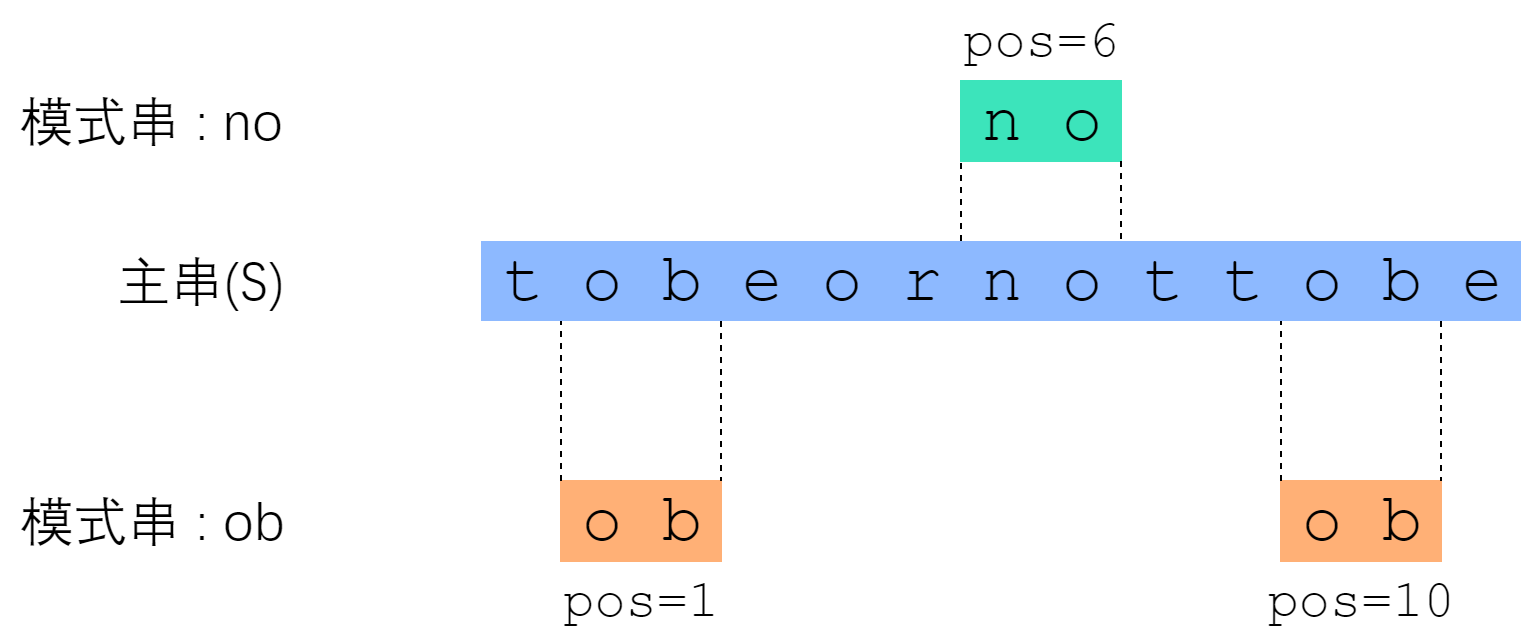
所谓字符串匹配, 是这样一种问题: “字符串 P 是否为字符串 S 的子串? 如果是, 它出现在 S 的哪些位置? ” 其中 S 称为主串; P 称为模式串. 下面的图片展示了一个例子
算法
Brute-Force(暴力法)
- 枚举 i = 0, 1, 2 … , len(S)-len(P)
- 将 S[i : i+len(P)] 与 P 作比较. 如果一致, 则找到了一个匹配.
现在我们来模拟 Brute-Force 算法, 对主串 “AAAAAABC” 和模式串 “AAAB” 做匹配:
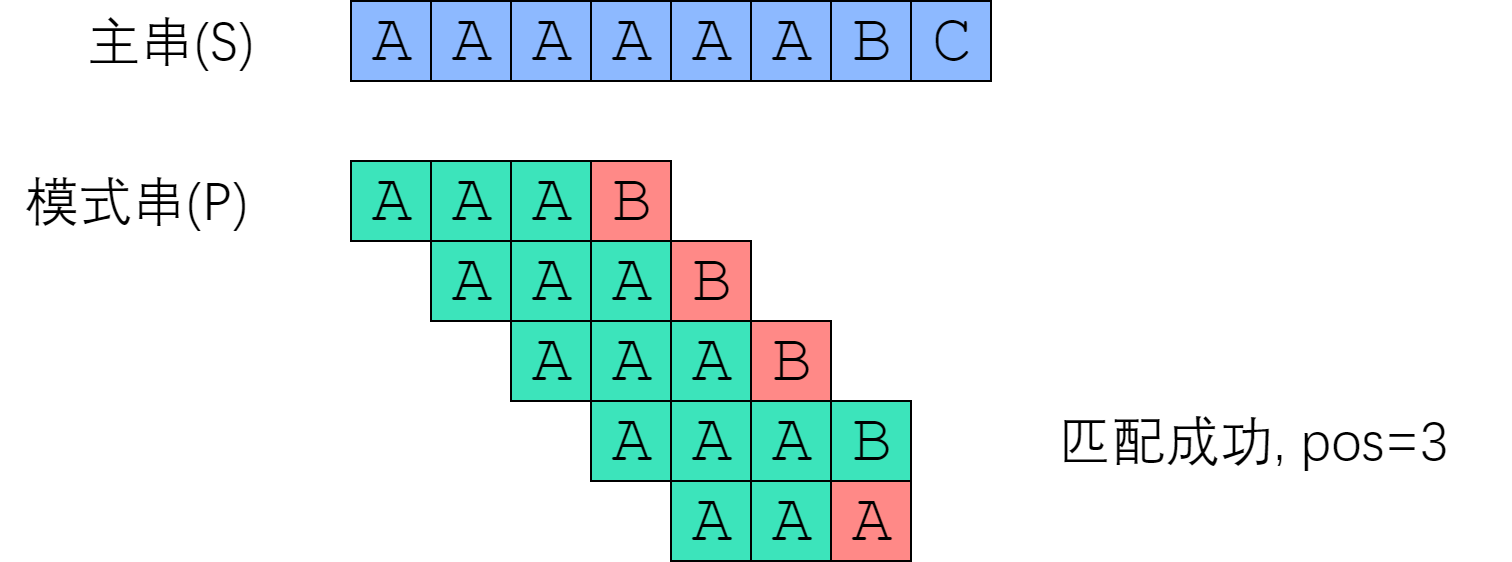
时间复杂度: O(nm)
KMP算法
理解下,Brute-Force算法的主要问题在于,s串需要回溯。并且模式串每次都需要从0位置开始比较。效率很低。其实可以通过快速对齐的方式来处理。如下图
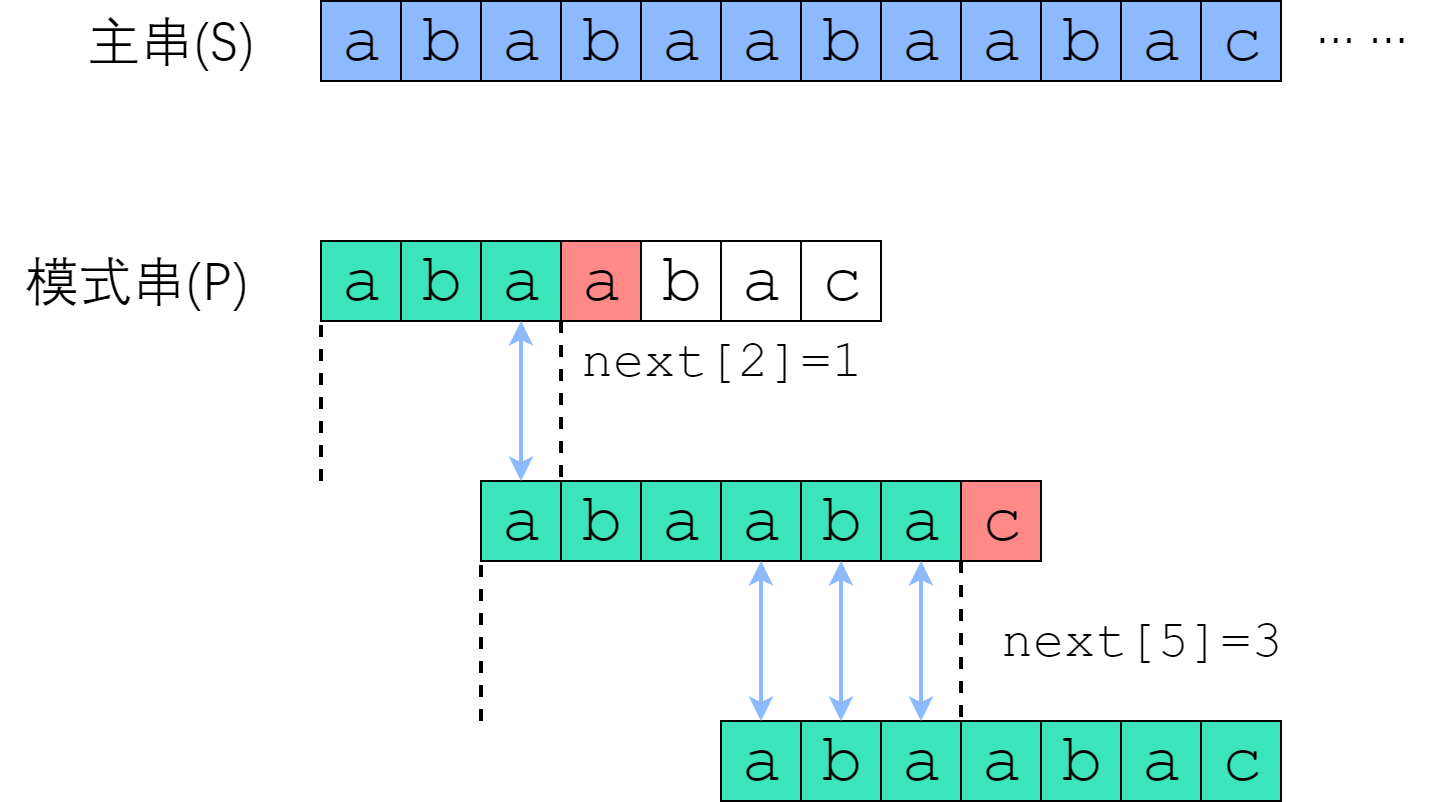
- 当netx[3]不匹配时,此时主串不回溯,将模式串的前缀部分能以已匹配的主串进行对齐比较,这样就无需回溯,并且模式串匹配变成了从1开始。 从上可知,其实就是S的不匹配之前的后缀 = P的前缀。即 P[0] 到 P[i] 这一段子串中, 前next[i]个字符与后next[i]个字符一模一样. 既然如此, 如果失配在 P[r], 那么P[0]~P[r-1]这一段里面, 前next[r-1]个字符恰好和后next[r-1]个字符相等——也就是说, 我们可以拿长度为 next[r-1] 的那一段前缀, 来顶替当前后缀的位置, 让匹配继续下去。
next数组的生成
快速构建next数组, 是KMP算法的精髓所在, 核心思想是”P自己与自己做匹配”.
- 定义 “k-前缀” 为一个字符串的前 k 个字符; “k-后缀” 为一个字符串的后 k 个字符. k 必须小于字符串长度.
- next[x] 定义为: P[0]~P[x] 这一段字符串, 使得k-前缀恰等于k-后缀的最大的k.
如果next[0], next[1], … next[x-1]均已知, 那么如何求出 next[x] 呢?
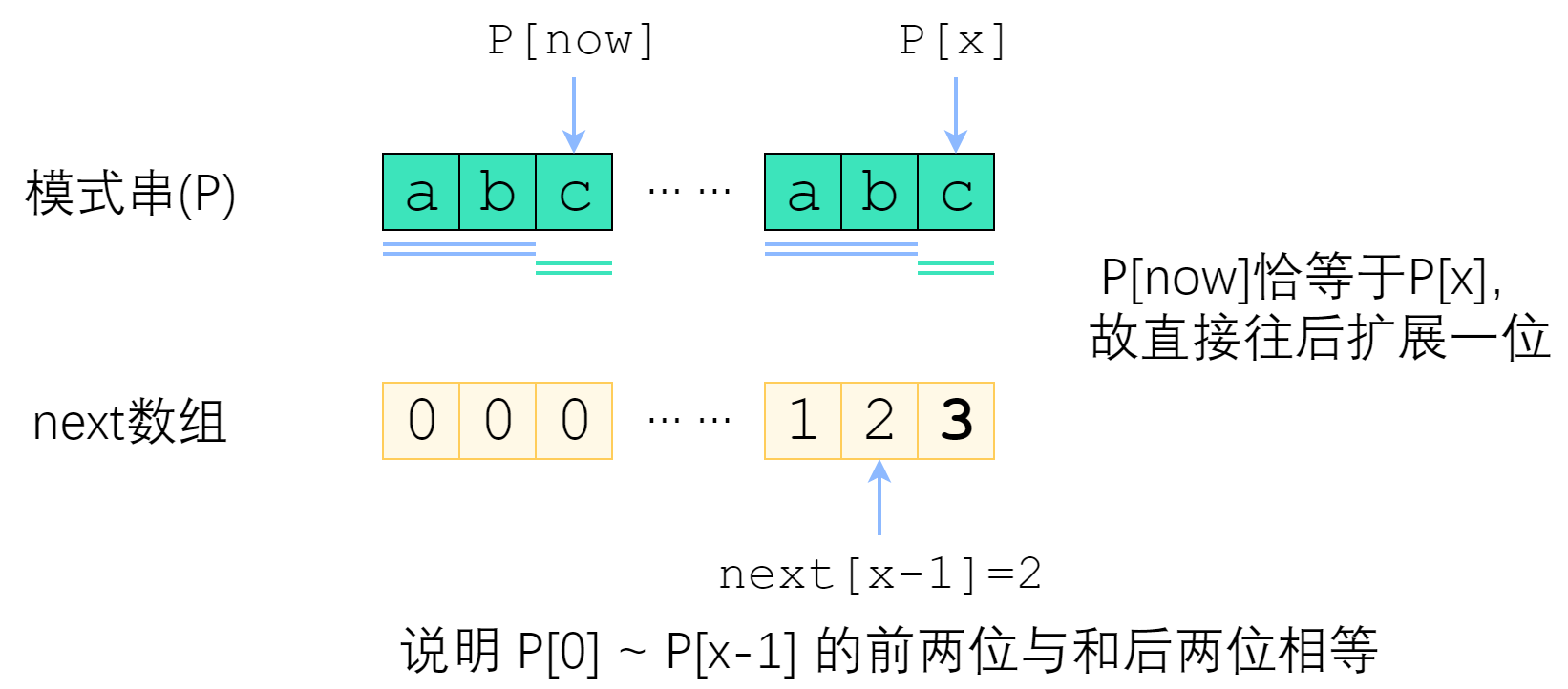
p[x] = p[now] 则next[x] = now +1
首先, 已经知道了 next[x-1] 以下记为now, 如果 P[x] 与 P[now] 一样, 那最长相等前后缀的长度就可以扩展一位, 很明显 next[x] = now + 1;
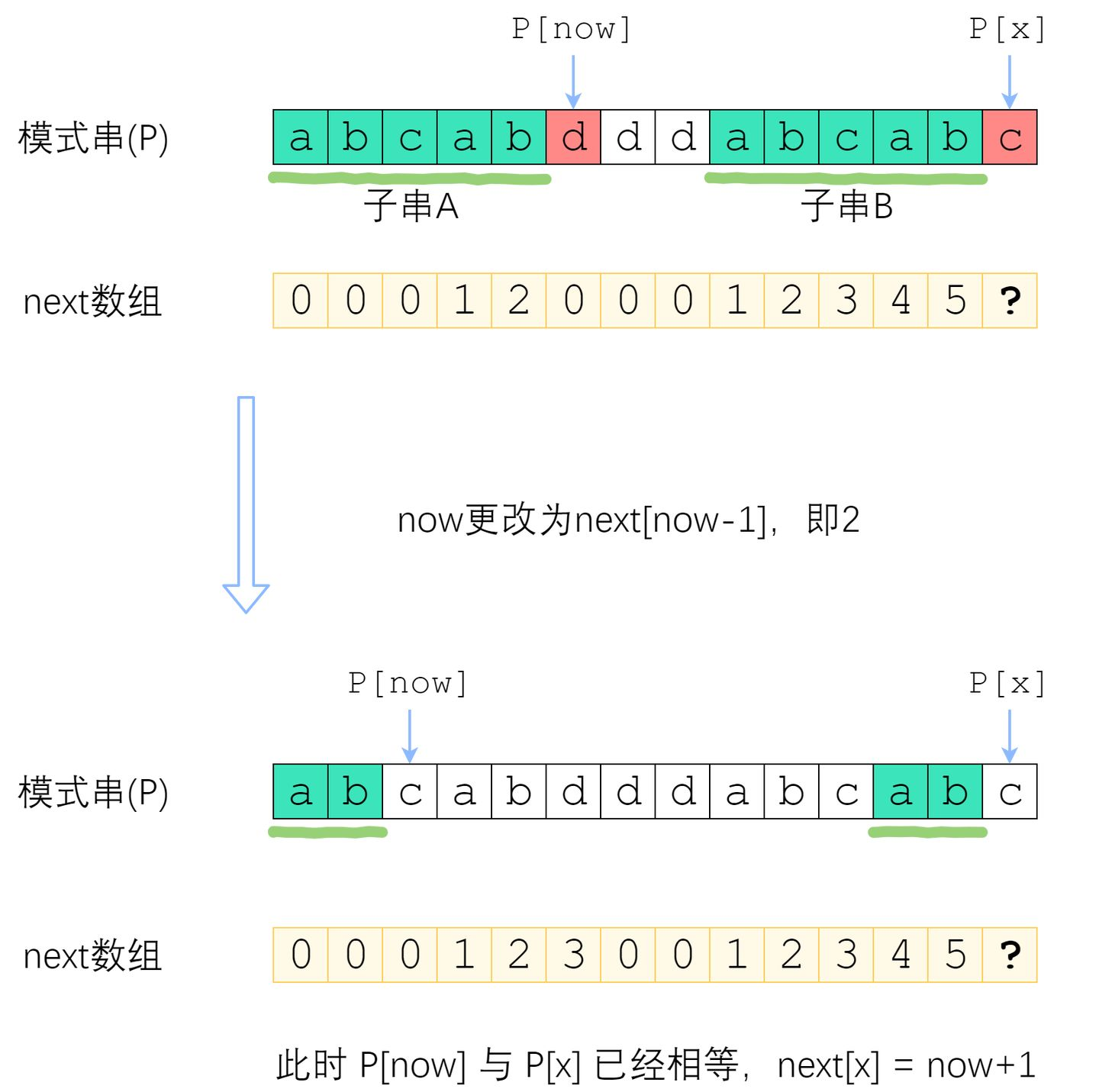
p[x] != p[now] 则 next[x] = next[now-1]
- 长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀. 可惜 A 右边的字符和 B 右边的那个字符不相等, next[x]不能改成 now+1 了. 因此, 我们应该缩短这个now, 把它改成小一点的值, 再来试试 P[x] 是否等于 P[now].
now该缩小到多少呢? 显然, 我们不想让now缩小太多. 因此我们决定, 在保持”P[0]~P[x-1]的now-前缀仍然等于now-后缀”的前提下, 让这个新的now尽可能大一点. P[0]~P[x-1] 的公共前后缀, 前缀一定落在串A里面, 后缀一定落在串B里面. 换句话讲: 接下来now应该改成: 使得 A的k-前缀等于B的k-后缀 的最大的k. 您应该已经注意到了一个非常强的性质——串A和串B是相同的! B的后缀等于A的后缀! 因此, 使得A的k-前缀等于B的k-后缀的最大的k, 其实就是串A的最长公共前后缀的长度 —— next[now-1]
推导过程:
- p[x] == p[now]
- next[x] = now +1
- p[x] != p[now] —> 要尽可能找到保持 P[0]~P[x-1]的now-前缀仍然等于now-后缀 下,now最大
- 因为为了求 p[x-1]的公共前后缀,前缀一定在子串A, 后缀一定在子串B。即命题转换成了,求 使得 A的k-前缀等于B的k-后缀 的最大的k
- 因为 串A = 串B. 所以 命题转换成了 求 串A的最长公共前后缀的长度。不就是等于now = next[now-1].
- 当P[now]与P[x]不相等的时候, 我们需要缩小now——把now变成next[now-1], 直到P[now]=P[x]为止. P[now]=P[x]时, 就可以直接向右扩展了。