算法 §

大O表示法 §

渐进符号 §

线性结构 §

线性存储 §

数组 §

一维数组 & 二维数组 §

FIRST_ADDR 首先地址 N行M列数组, L 每个元素大小

按行存储: a_i,j = FIRST_ADDR + (i * M + j) * L

按列存储: a_i,j = FIRST_ADDR + (j * N + i) * L

对角矩阵(对角对称) §

1 2 3
2 3 4
3 4 5

有多少行:
1 + 2 + 3 + n = (1 + n)* n /2

三对角矩阵(边角都是0) §

稀疏矩阵(大部分都是0) §

队列 §

栈 §

链式存储 §

KMP算法 §

KMP算法

树 §

根节点: 没有入度，可以有多个出度
其它节点(内部节点): 只有1个入度。可以有多个出度。
度: 一个节点的子节点的个数
叶子节点: 出度为0的节点。

层数: 根节点是1层，从1算起。
树的高度: 即一棵树最大的层数。

二叉树 §

与树最大的区别就是，每个根节点最多左右2个子节点

分类 §

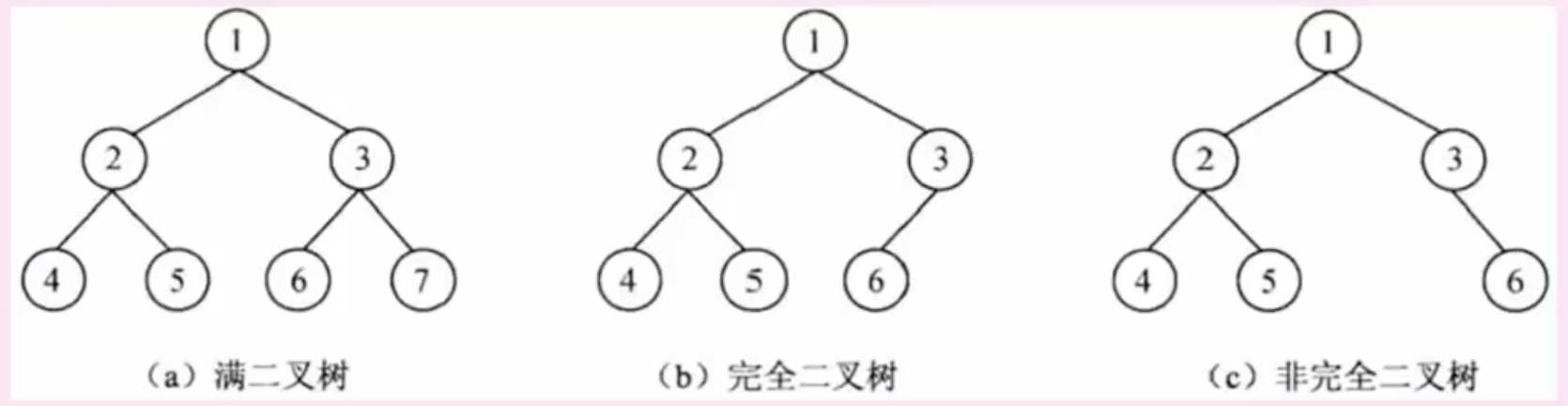
满二叉树: 每一层都是满的
完全二叉树: k-1层是满节点，k层(最底层)从左到右是满的
非完全二叉树:

规则 §

1. 第n层的个数为 2^^n-1
2. 高度为k的二叉树，总共有 2^k-1个节点
3. 完全二叉树能容纳的节点为n，则共有 (log₂n) +1 层

二叉树的存储结构 §

顺序存储(数组) §

链式存储 §

二叉树的遍历 §

• 这里说的前中后，是以根节点的访问顺序可分为
  前序遍历: 根左右
  中序遍历: 左根右
  后续遍历: 左右根

• 层次遍历法:

  • 从左到右。
  • 从上到下

平衡二叉树 §

左右子树的高度的绝对值<=1

线索二叉树 §

最优二叉树(哈夫曼树) ⭐ 🔢 ❓ §

路径: 树中一个节点到另外一个节点之间的通路
树的路径长度: 根节点到达每一个叶子节点之间的路径长度之和
树的带权路径长度: 每个路径长度带有权，即加权和

树和森林 ❓ §

查找二叉树 ❓ §

为了方便查找
左 < 根 < 右

二叉树的查找，取决于树的深度。对于节点相同的二叉树，平衡二叉树深度最小。

根据前中后遍历，推二叉树

图 §

无向图: 节点直接的联系是没有方向的。领接是对称矩阵
有向图: 有方向。
路径： 可以走通就可以
边: 要存在

无相连通图: 任意2个顶点都存在路径，
强连通图: 任意2个顶点，都有边

图的存储 §

完全图: 边多

邻接矩阵 §

以边的数量为矩阵的规模。无向图，只需存储一半

邻接链表 §

相邻的作为链表

图的遍历 §

复杂度: §

领接矩阵: O(n²)
领接链表: O( n + e)

深度优先 §

广度优先（类似于层次遍历，可以用队列） §

图的最小生成 ❓ §

拓扑排序 §

AOV网（有向无环图） §

类似与pmp的

如果判断有无环？

1. 找出入度为0的顶点
2. 删除与这个顶点相关的边
3. 重复上述2个步骤。

2个定律。如果一个拓扑序列为 6 4 2 1 3

1. 可能 6 —> 3的边，但是一定不存在 3 —> 6的边
2. 可能存在 6—> 3的路径，一定不存在 3—> 6 的路

查找 §

静态查找: 顺序查找，折半查找，分块查找
动态查找: 二叉排序树、平衡二叉树、B-树、哈希树

顺序查找 §

平均查找长度: (n+1)/2

折半查找 §

最多比较次数: (log₂N ) 向下取整+1。即这种树的深度。
平均查找长度: (log₂ (N+1)) -1

二分查找

哈希 §

哈希表，重点在于 1. 哈希函数，2， 哈希冲突处理

哈希函数 §

直接地址法、数字分析法、平方取中法、折叠法、随机数法
除留取余法 H(key) = key %m; m取接近1但是不大于key的质素。

哈希冲突 §

开发地址法:
1. 线性探测法， 找下一个 . di = 1,2,3, …
2. 二次探测法: di = 1² -1² 2² -2² 3² -3²
链地址法: java中的map

哈希查找 §

装填因子: 已装入元素/哈希表的长度。

大顶堆与小顶堆 §

排序 §